揭秘三角形ABC:60度角B与角平分线AD、CE的奇妙交汇点
在一个有趣的几何世界里,有一个特别的三角形,我们称之为ABC。这个三角形有一个非常醒目的特点:它的角B恰好是60度。想象一下,你手里拿着一块等边三角形的饼干,轻轻咬掉一个小角,留下的大致就是ABC的形状,只不过角B依旧保持着完美的60度。现在,让我们一起探索这个三角形内部的一个神秘交点——当它的两条角平分线AD和CE相遇时,会发生什么奇妙的事情呢?
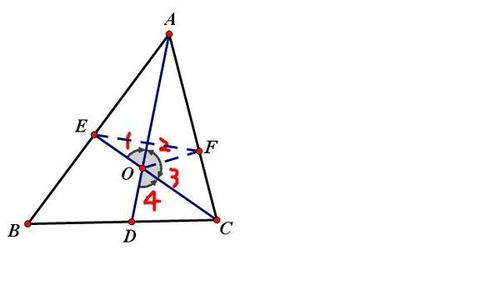
角平分线的魔法
首先,让我们来理解什么是角平分线。简单来说,角平分线就是从三角形的一个角的顶点出发,将该角平分为两个相等的小角的那条线。在三角形ABC中,AD是角BAC的平分线,它均匀地将角BAC分为两个较小的、相等的角;同样地,CE是角ACB的平分线,它也执行着相同的任务。

现在,想象一下这两条神奇的线在三角形内部交织,它们在某个点O交汇。这个点O,就像是一个小小的几何魔法师,连接着三角形的两个重要部分。在数学上,这样的交点被称为三角形的内心或者角平分线的交点。但在这个故事中,我们更愿意把它想象成一个藏着无数秘密的小小宝藏箱。

60度角的特殊意义
为什么角B是60度如此重要呢?原因在于,60度是一个既特殊又和谐的角度。它是等边三角形的一个内角,意味着如果三角形ABC的其他两个角也都是60度,那么它就是一个完美的等边三角形。但即使只有角B是60度,这个角度也为三角形ABC带来了一些独特的性质,尤其是在考虑角平分线交点O的时候。
探索交点O的奇妙性质
1. 等面积四边形:
当我们把注意力集中在交点O上时,一个有趣的发现是,通过O点可以构造出一个特殊的四边形——AODE(其中D是AD与BC的交点,E是CE与AB的交点)。这个四边形有一个令人惊讶的性质:它的面积等于三角形ABC的一半!这是因为角平分线的性质确保了从O点到三角形三边的垂线段(即高)是相等的,从而使得四边形AODE与三角形ABC在面积上有着特定的比例关系。
2. 角度的和谐:
除了面积上的特性,交点O还与角度有着不解之缘。由于AD和CE是角平分线,它们分别将角BAC和角ACB分为两个相等的部分。更神奇的是,当角B为60度时,通过一系列几何证明,我们可以发现∠AOE(即O点处的外角,由OA和OE构成)也恰好是120度。这个角度的和谐性,进一步增强了三角形ABC内部的几何美感。
3. 内心的几何中心:
交点O不仅是角平分线的交点,还是三角形ABC的内心。内心是三角形三条内角平分线的交点,它具有一些特殊的性质,比如到三角形三边的距离相等。在角B为60度的三角形ABC中,这一性质表现得尤为明显,因为内心的存在使得三角形内部的几何结构更加均衡和对称。
4. 构造等边三角形:
更有趣的是,通过O点,我们可以构造出与三角形ABC相关的等边三角形。例如,以O为圆心,OA或OC为半径画圆,这个圆会与三角形ABC的三边相切于三个点,这三个点与O点相连,就能得到一个与三角形ABC有特定关系的等边三角形。这一构造不仅展示了60度角的强大威力,也揭示了三角形内部隐藏的几何宝藏。
实际应用与想象空间
虽然这些关于三角形ABC、角平分线交点O以及60度角的性质听起来有些抽象,但它们在数学、物理乃至工程设计中都有着广泛的应用。比如,在计算机图形学中,了解这些性质可以帮助我们更高效地生成和处理几何图形;在建筑设计中,利用这些性质可以设计出更加美观和稳定的结构。
此外,这些几何性质也为我们的想象空间提供了无限的素材。想象一个充满奇幻色彩的几何世界,在这里,三角形ABC和它的角平分线交点O是通往另一个维度的门户。通过探索这个门户,我们可以发现更多关于形状、空间和时间的秘密。
结语
总之,三角形ABC中的角B为60度,以及它的两条角平分线AD和CE相交于O点,为我们打开了一个充满奇妙性质和无限想象空间的几何世界。在这里,我们不仅可以学到关于面积、角度和几何中心的有趣知识,还可以激发我们对数学和物理世界的探索热情。所以,下次当你在数学课本上看到这样的三角形时,不妨停下来,仔细观察并思考它背后的故事和秘密吧!
- 上一篇: 揭秘!圭贤与宋茜之间的神秘关系
- 下一篇: 如何合法访问受限的QQ空间内容?
-
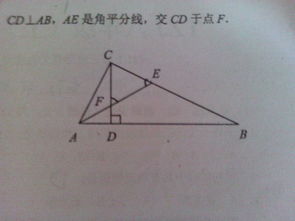 三角形ABC中,角平分线CD与边BC、AC的关系探究资讯攻略03-26
三角形ABC中,角平分线CD与边BC、AC的关系探究资讯攻略03-26 -
 造梦西游3修改大师v3.0.9.7豪华版:CE修改失效大揭秘!资讯攻略03-14
造梦西游3修改大师v3.0.9.7豪华版:CE修改失效大揭秘!资讯攻略03-14 -
 揭秘“堡”字的多音读法:两种发音全解析资讯攻略01-07
揭秘“堡”字的多音读法:两种发音全解析资讯攻略01-07 -
 等腰三角形一腰中线有什么性质或作用?资讯攻略11-26
等腰三角形一腰中线有什么性质或作用?资讯攻略11-26 -
 Win7用户首选:智能ABC输入法官方下载资讯攻略11-26
Win7用户首选:智能ABC输入法官方下载资讯攻略11-26 -
 掌握秘籍!造梦西游3修改器CE高效使用指南资讯攻略03-26
掌握秘籍!造梦西游3修改器CE高效使用指南资讯攻略03-26











