等腰三角形一腰中线有什么性质或作用?
等腰三角形一腰上的中线:几何世界的奇妙桥梁
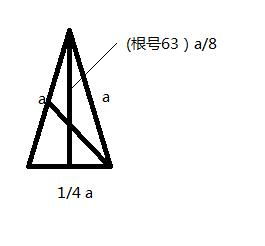
在几何学的浩瀚宇宙中,等腰三角形以其独特的对称美吸引着无数探索者的目光。而在等腰三角形的众多性质中,一腰上的中线更是隐藏着一系列令人着迷的秘密。今天,就让我们一同踏上这场探索之旅,揭开等腰三角形一腰上的中线所蕴含的奥秘。
首先,我们需要明确等腰三角形的定义。等腰三角形是指两边长度相等的三角形,这两条相等的边被称为等腰三角形的腰。在等腰三角形中,由于两边相等,其对应的两个底角也相等,这使得等腰三角形具有一种天然的对称美。
当我们把目光投向等腰三角形的一腰时,会发现一个有趣的点——这条腰的中点。中点,顾名思义,就是线段上距离两端点距离相等的点。在等腰三角形中,如果我们取一条腰的中点,并连接这个中点和三角形的顶点(非这条腰的两个端点之一),就会得到一条新的线段,我们称之为等腰三角形一腰上的中线。
这条中线,看似简单,实则蕴含着丰富的几何性质。首先,它是一条特殊的线段,因为它不仅连接了等腰三角形的一个顶点和一条腰的中点,还具备了一些独特的性质。
性质一:中线长度与底边关系
在等腰三角形中,一腰上的中线与底边之间有着密切的关系。具体来说,这条中线的长度是底边长度的一半再乘以根号下三再除以二(即底边长度的一半乘以根号三的二分之一)。这个性质可以通过简单的几何证明得出,它揭示了等腰三角形一腰上的中线与底边之间的比例关系。
性质二:中线与底边平行线的交点
除了与底边的直接关系外,等腰三角形一腰上的中线还与底边的平行线有着特殊的交点。如果我们过等腰三角形的顶点作底边的平行线,并延长这条中线与之相交,那么交点、顶点和中点三点共线。这个性质同样可以通过几何证明得出,它进一步展示了等腰三角形一腰上的中线在几何世界中的独特地位。
性质三:中线与等腰三角形的对称性
等腰三角形本身就是一种对称的图形,而一腰上的中线更是这种对称性的体现。如果我们沿着这条中线将等腰三角形对折,那么两侧的图形会完全重合。这种对称性不仅使得等腰三角形在视觉上更加美观,还为我们解决一些几何问题提供了便利。
性质四:中线与三角形内角的关系
在等腰三角形中,一腰上的中线还与三角形的内角有着密切的关系。具体来说,这条中线将等腰三角形的一个顶角平分为两个相等的角。这个性质可以通过角的平分线性质以及等腰三角形的性质共同得出。它揭示了等腰三角形一腰上的中线在角度方面的独特作用。
性质五:中线与三角形面积的关系
在等腰三角形中,一腰上的中线还与三角形的面积有着密切的关系。如果我们知道等腰三角形的腰长、底边长以及高(或中线长),就可以通过这些信息计算出三角形的面积。具体来说,我们可以利用三角形的面积公式(面积等于底乘以高的一半)以及中线与底边和高之间的关系来求解。这个性质为我们提供了一种计算等腰三角形面积的新方法。
除了以上这些性质外,等腰三角形一腰上的中线还与一些其他的几何概念有着紧密的联系。例如,它与三角形的中位线、三角形的角平分线以及三角形的中线族等都有着千丝万缕的关系。这些关系不仅丰富了我们对等腰三角形一腰上的中线的认识,还为我们解决一些复杂的几何问题提供了有力的工具。
在实际应用中,等腰三角形一腰上的中线也发挥着重要的作用。例如,在建筑设计中,我们经常会遇到需要构建对称结构的情况。这时,我们就可以利用等腰三角形一腰上的中线的对称性来设计出既美观又实用的建筑方案。此外,在机械制造、电子电路设计等领域中,等腰三角形一腰上的中线也经常被用作设计参考线或基准线来确保产品的精度和稳定性。
当然,对于等腰三角形一腰上的中线的探索并不仅仅停留在理论层面。在实际的数学教学中,我们也可以通过一些有趣的实验和实践活动来让学生更加直观地感受这条中线的魅力。例如,我们可以让学生自己动手制作一些等腰三角形的模型,并通过测量和计算来验证上述性质。这样的实践活动不仅可以激发学生的学习兴趣和动手能力,还可以帮助他们更好地理解和掌握几何知识。
总之,等腰三角形一腰上的中线是几何世界中的一座奇妙桥梁。它连接着等腰三角形的顶点与腰的中点,同时也连接着几何学的众多概念和性质。通过深入探索这条中线所蕴含的奥秘,我们不仅可以更加全面地认识等腰三角形这一几何图形,还可以为数学学习和实践应用提供有力的支持和帮助。让我们继续前行,在几何学的广阔天地中不断探索、不断发现、不断成长!
- 上一篇: 大庆个人公积金账户如何查询?
- 下一篇: 研究生求职为何屡屡碰壁?揭秘背后原因!
-
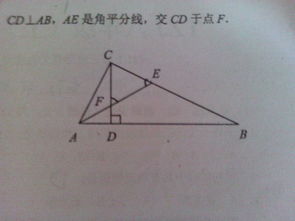 三角形ABC中,角平分线CD与边BC、AC的关系探究资讯攻略03-26
三角形ABC中,角平分线CD与边BC、AC的关系探究资讯攻略03-26 -
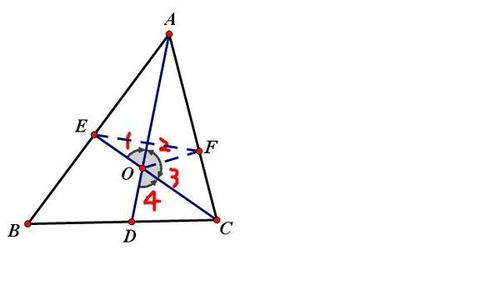 揭秘三角形ABC:60度角B与角平分线AD、CE的奇妙交汇点资讯攻略01-22
揭秘三角形ABC:60度角B与角平分线AD、CE的奇妙交汇点资讯攻略01-22 -
 泡沸石是什么?介绍一下资讯攻略03-12
泡沸石是什么?介绍一下资讯攻略03-12 -
 尿素:为何成为最广泛施用的氮肥之选?资讯攻略11-29
尿素:为何成为最广泛施用的氮肥之选?资讯攻略11-29 -
 探索高中数学必修5:解锁数学奥秘之旅资讯攻略03-12
探索高中数学必修5:解锁数学奥秘之旅资讯攻略03-12 -
 辐射是如何影响人体的?资讯攻略03-01
辐射是如何影响人体的?资讯攻略03-01












