三角形ABC中,角平分线CD与边BC、AC的关系探究
已知:如图,在三角形ABC中,CD是三角形ABC的角平分线,BC>AC,点E在BC上,且DE∥AC,点F在AC上,且EF=EC。求证:四边形CDEF是等腰梯形。
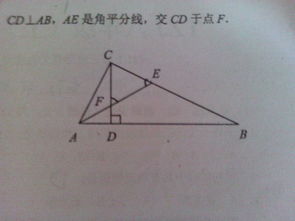
我们可以按照以下的思路进行分析:

第一步,根据已知条件,CD是三角形ABC的角平分线,所以∠ACD=∠BCD。

第二步,由于DE∥AC,根据平行线的性质,我们知道交替内角相等,即∠CDE=∠ACD。

第三步,由第一步和第二步的结论,我们可以得出∠CDE=∠BCD。
第四步,根据等腰三角形的性质,若在三角形中,一个角与其相邻的一个外角相等,则与这个角相对的两边相等。所以,在三角形CDE中,CE=DE。
第五步,已知EF=EC,所以EF=DE。
第六步,由于DE∥AC,根据平行四边形的性质,若四边形中有一组对边平行且相等,则这个四边形是平行四边形。但在这里,虽然DE∥AC且DE=EF,但EF并不与CD平行,所以四边形CDEF不是平行四边形。然而,由于它有一组对边平行(DE∥AC,即DE∥CF,因为F在AC上)且这组对边相等(DE=EF),所以四边形CDEF是等腰梯形。
综上,我们证明了四边形CDEF是等腰梯形。
在解决这个问题的过程中,我们深入了解了角平分线、平行线、等腰三角形以及等腰梯形的性质。接下来,我们将进一步探讨这些性质以及它们在数学和几何中的应用。
角平分线,作为几何中的一个基本概念,它将一个角分为两个相等的小角。在三角形中,角平分线从一个角的顶点出发,将对边分为两部分,与这个角相邻的两边所形成的两个小三角形面积之比等于这两边之比。在本题中,CD作为三角形ABC的角平分线,将∠ACB分为两个相等的角∠ACD和∠BCD,这是解题的关键一步。
平行线,在几何学中,指的是在同一平面内永不相交的两条直线。平行线的性质在解题中经常被用到,如交替内角相等、同位角相等、内错角相等。在本题中,DE∥AC,使得我们可以利用平行线的性质得出∠CDE=∠ACD。
等腰三角形,是指两边相等的三角形。在等腰三角形中,两个底角相等,顶角的角平分线、底边上的中线、底边上的高互相重合。在本题中,虽然我们没有直接构造等腰三角形,但利用了等腰三角形的性质(一个角与其相邻的一个外角相等,则与这个角相对的两边相等)来证明CE=DE。
等腰梯形,是指一组对边平行且不相等,另一组对边不平行但相等的四边形。等腰梯形的性质包括:等腰梯形的两条对角线相等;等腰梯形在同一底上的两个角相等;等腰梯形的中线(连接两条对角线的中点的线)等于上底加下底和的一半。在本题中,我们证明了四边形CDEF满足等腰梯形的定义和性质,即有一组对边平行(DE∥CF)且这组对边相等(DE=EF)。
除了上述性质外,本题还涉及到了线段相等的证明。在几何学中,证明线段相等是常见的题型。常用的方法有:利用全等三角形的对应边相等;利用等腰三角形的性质;利用线段垂直平分线的性质;利用平行四边形、矩形、菱形、正方形、等腰梯形等的对角线性质;利用相似三角形的对应边成比例;利用比例式或等积式化归;利用三角形的中位线定理。在本题中,我们主要利用了等腰三角形的性质来证明线段CE和DE相等。
此外,本题还涉及到了平行四边形的判定。平行四边形的判定方法有五种:两组对边分别平行的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;两组对角分别相等的四边形是平行四边形。虽然本题中的四边形CDEF不是平行四边形,但我们在解题过程中考虑到了平行四边形的判定方法,以确保我们的证明过程严谨无误。
综上所述,本题通过证明四边形CDEF是等腰梯形,让我们深入了解了角平分线、平行线、等腰三角形以及等腰梯形的性质。同时,也锻炼了我们运用这些性质进行几何证明的能力。在解题过程中,我们需要灵活运用各种几何性质和判定方法,以确保证明过程的严谨性和正确性。通过不断的练习和思考,我们可以进一步提高自己的几何素养和解题能力。
- 上一篇: 魔兽世界80级全火法天赋怎么加点?
- 下一篇: 揭秘:手机电池寿命衰减的真相,为何越用越不耐用?
-
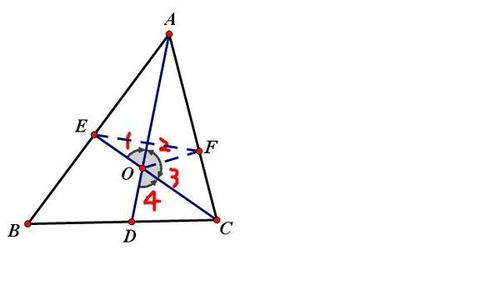 揭秘三角形ABC:60度角B与角平分线AD、CE的奇妙交汇点资讯攻略01-22
揭秘三角形ABC:60度角B与角平分线AD、CE的奇妙交汇点资讯攻略01-22 -
 探索高中数学必修5:解锁数学奥秘之旅资讯攻略03-12
探索高中数学必修5:解锁数学奥秘之旅资讯攻略03-12 -
 三角围巾系法指南资讯攻略03-24
三角围巾系法指南资讯攻略03-24 -
 清华紫光拼音与智能ABC输入法,哪个更胜一筹?资讯攻略11-28
清华紫光拼音与智能ABC输入法,哪个更胜一筹?资讯攻略11-28 -
 将CD-ROM光驱改造成私人CD播放器教程资讯攻略01-25
将CD-ROM光驱改造成私人CD播放器教程资讯攻略01-25 -
 Win7用户首选:智能ABC输入法官方下载资讯攻略11-26
Win7用户首选:智能ABC输入法官方下载资讯攻略11-26












