揭秘函数符号背后的有趣故事
函数符号的奇妙之旅

在数学的世界里,符号不仅仅是简单的标记,它们更像是通往另一个维度的钥匙,解锁着宇宙的奥秘与自然的规律。其中,函数符号,这一串串看似无序却蕴含无限可能的字符组合,正是这场数学探险中不可或缺的向导。它们不仅承载着数学家们的智慧与灵感,更在历史的长河中,编织出一个个引人入胜的故事。

故事要从古希腊时代说起,那时的数学家们已经开始思考变量之间的关系,虽然他们尚未明确提出“函数”这一概念,但他们的思想已经为后世函数理论的发展奠定了基石。毕达哥拉斯学派研究的音乐与数学之间的关系,以及后来的几何学家们对曲线的研究,都隐含着函数关系的萌芽。然而,直到17世纪,随着微积分的诞生,函数这一概念才正式登上历史的舞台。

莱布尼茨,这位德国-瑞士的数学家和哲学家,被誉为微积分的共同创始人之一,他在1673年首次使用了“function”(函数)这个词,用来描述一个量随另一个量变化的关系。莱布尼茨的函数观念相当广泛,他认为“一个变量的值随另一个变量的值而变化,或者一个量包含另一个量”,这构成了函数的基本定义。而在符号表达上,莱布尼茨引入了“f(x)”这样的形式来表示函数,其中f代表函数,x代表自变量,这一符号体系至今仍为数学界所沿用,成为函数表达的标准形式。
但函数符号的演变并未止步于莱布尼茨的f(x)。随着数学研究的深入,特别是随着分析学、几何学以及物理学的快速发展,越来越多的函数形式被发现,它们各自具有独特的性质和用途。于是,数学家们开始为这些特殊函数设计专门的符号,以便更准确地描述它们的行为。
例如,欧拉,这位瑞士出生的数学家,被誉为18世纪最伟大的数学家之一,他对函数符号的贡献尤为显著。欧拉不仅在数学分析、几何学和力学等领域做出了卓越贡献,还在函数符号的标准化和简化方面发挥了重要作用。他引入了诸如e(自然对数的底数)、π(圆周率)、i(虚数单位)等著名的数学常数和符号,并创造性地使用了诸如sin(x)、cos(x)等来表示三角函数,这些符号不仅简洁明了,而且易于记忆和运算,极大地推动了数学的发展。
欧拉在函数符号上的另一个重要贡献是,他发展了函数的表示方法,特别是无穷级数和无穷乘积的表示方法。这些表示方法使得数学家们能够更深入地研究函数的性质,包括它们的奇偶性、周期性、单调性等,同时也为求解复杂的数学问题提供了新的工具和思路。
随着19世纪的到来,数学的发展进入了一个新的阶段。在这一时期,实数理论、复变函数论、微分方程理论等分支学科相继建立和发展起来,函数的概念和符号也随之得到了进一步的丰富和完善。特别是黎曼和魏尔斯特拉斯等数学家对函数定义的深化,使得函数不再仅仅局限于实数域内的对应关系,而是可以扩展到更广泛的数学结构中,如复数域、向量空间、乃至更一般的拓扑空间等。
在这一时期,函数符号的使用也变得更加灵活和多样化。例如,为了表示复杂的函数关系,数学家们引入了复合函数符号f(g(x)),以及反函数符号f⁻¹(x)等。同时,随着计算机科学的兴起和数学软件的发展,函数符号的输入和显示方式也变得更加便捷和直观,这进一步促进了数学研究的深入和普及。
进入21世纪,函数符号的故事仍在继续。随着大数据、人工智能等技术的快速发展,数学和计算机科学之间的界限越来越模糊,函数作为描述数据之间关系的强大工具,其重要性也日益凸显。在这个时代,数学家们和计算机科学家们正在共同努力,探索更加高效、准确和智能的函数表示方法,以应对日益复杂的实际问题。
回顾函数符号的演变历程,我们不难发现,它不仅是数学发展的缩影,更是人类智慧和创新精神的体现。从莱布尼茨的f(x)到欧拉的sin(x)和cos(x),再到现代数学中复杂多样的函数符号体系,每一个符号的引入和演变,都凝聚着数学家们的辛勤付出和深刻洞察。
而在这个过程中,函数符号也悄然改变了我们的世界。它们不仅是数学研究中的得力助手,更是科学探索、工程实践、数据分析等领域中不可或缺的工具。通过函数符号,我们能够更准确地描述和预测自然现象,解决复杂问题,推动科技的进步和社会的发展。
展望未来,函数符号的故事仍将充满无限可能。随着数学和其他学科的交叉融合,我们有理由相信,函数符号将会继续演变和发展,为我们揭示更多宇宙的奥秘,创造更加美好的未来。在这个过程中,我们每个人都可以成为这个故事的见证者和参与者,通过学习和探索,共同书写函数符号的新篇章。
- 上一篇: 探索WLK版本:打造传奇附魔戒指的秘密
- 下一篇: 想知道雅芳保湿凝露的锁水秘密?保湿效果究竟如何?
-
 揭秘“芒果台”昵称的由来,背后故事竟如此有趣!资讯攻略11-19
揭秘“芒果台”昵称的由来,背后故事竟如此有趣!资讯攻略11-19 -
 轻松添加项目:使用 InsertItem() 函数资讯攻略12-03
轻松添加项目:使用 InsertItem() 函数资讯攻略12-03 -
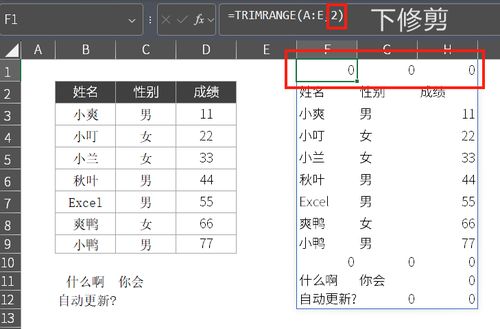 Excel函数:精简字符串(TRIM)资讯攻略12-07
Excel函数:精简字符串(TRIM)资讯攻略12-07 -
 轻松解决!“无法访问G盘:函数不正确”错误怎么办?资讯攻略11-25
轻松解决!“无法访问G盘:函数不正确”错误怎么办?资讯攻略11-25 -
 揭秘:0 FFFFFFFFC000034与0 0000000000背后的故事是什么?资讯攻略12-05
揭秘:0 FFFFFFFFC000034与0 0000000000背后的故事是什么?资讯攻略12-05 -
 骷髅头是哪个品牌的标志?资讯攻略12-03
骷髅头是哪个品牌的标志?资讯攻略12-03










